
main.py
import random
from fractions import Fraction
def enc(p, n, key1, key2):
q = (Fraction(p, n+1)*key1**(n+1)) - (Fraction(p, n+1)*key2**(n+1))
print("[OK] plain is encrypted : ", q)
return q
def dec(q):
# cencored
def key_make():
n, key1, key2 = 0, 1, 0
while key2 < key1:
n = random.randrange(1, 10)
key1 = random.randrange(1, 100)
key2 = random.randrange(1, 100)
return n, key1, key2
p = ""
emp = input("plain text: ")
for character in emp:
p += str(ord(character))
n, key1, key2 = key_make()
print(f"[WAR]p = {p} n = {n} key1 = {key1} key2 = {key2}")
q = enc(int(p), n, key1, key2)
dec(q)
readme.txt
n = 3
key 1 = #cencored#
key 2 = 95
q = -200640142664324295933714
p = #cencored# (p is number)
if you get the p(decrypted q)
plz enter the p in the DH{here}
https://velog.io/@jh_0517/Dream-Hack-write-up1
Dream Hack write-up(1)
ICM2022 🍇LEVEL 1 : Crypto > 문제 정보 Integral Cipher Master 2022 알고리즘을 사용하여 flag를 암호화 한것같은데… 복호화 할때 중요한 키와 복호화 코드를 실수로 지워버렸어요 암호화 된 flag를 다시 복
velog.io
이 코드는 수학적으로 암호화된 값 q에서 원래의 값 p를 복구하려는 과정을 나타냅니다. 주어진 코드를 단계별로 분석하고, 왜 이렇게 작성되었는지 설명하겠습니다.
코드 분석
변수의 의미
- n: 특정 상수 값으로, p를 암호화하는 데 사용된 지수입니다.
- key1, key2: 암호화에 사용된 두 개의 키로, 암호화와 복호화 과정에서 중요한 역할을 합니다.
- q: 암호화된 값입니다. 이 값을 이용해 p를 역으로 복구하려고 합니다.
- p: 복구하려는 원래 값입니다.
암호화 과정
암호화된 값 q는 다음 수식으로 생성된 것으로 보입니다:
q=(pn+1)⋅(key1n+1−key2n+1)q = \left( \frac{p}{n+1} \right) \cdot (key1^{n+1} - key2^{n+1})
여기서:
- pn+1\frac{p}{n+1}: 원래 값 p를 암호화하기 위한 정규화된 값.
- key1n+1−key2n+1key1^{n+1} - key2^{n+1}: 암호화를 위한 키 간의 차이의 n+1n+1제곱.
복호화 과정
복호화하려면 위의 수식을 변형해 p를 찾아야 합니다:
p=q⋅(n+1)key2n+1−key1n+1p = \frac{q \cdot (n+1)}{key2^{n+1} - key1^{n+1}}
- 분모:
- key2n+1−key1n+1key2^{n+1} - key1^{n+1}: 두 키의 n+1n+1제곱의 차이입니다.
- 분자:
- q⋅(n+1)q \cdot (n+1): 암호화된 값에 n+1n+1을 곱해 원래 값을 복구하는 데 사용.
코드의 역할
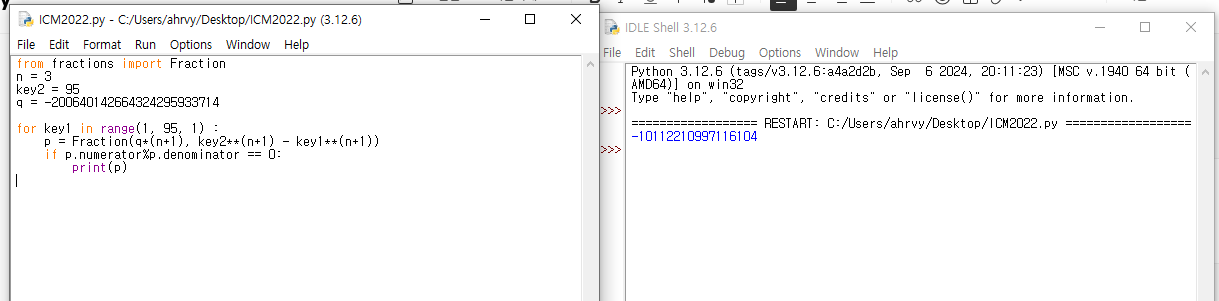
- for key1 in range(1, 95, 1):
- key1을 1부터 94까지 순차적으로 증가시키며 가능한 값을 모두 테스트합니다.
- p = Fraction(q*(n+1), key2**(n+1) - key1**(n+1))
- p를 분수로 계산합니다. 이때 분모가 key2n+1−key1n+1key2^{n+1} - key1^{n+1}이고, 분자가 q⋅(n+1)q \cdot (n+1)입니다.
- Fraction을 사용하면 정확한 분수로 계산할 수 있습니다.
- if p.numerator % p.denominator == 0:
- p의 분모로 분자를 나눈 나머지가 0인지 확인합니다. 이 조건은 p가 정수인지 확인하는 과정입니다.
- print(p)
- 정수 값인 p를 출력합니다.
왜 이런 접근을 사용했는가?
- 브루트포스 탐색: key1이 불확실하기 때문에 가능한 값(1부터 94)을 모두 시도해 적합한 값을 찾습니다.
- 분수 연산: Fraction을 사용해 나눗셈을 정확히 처리하고, 나머지가 0일 때만 p를 출력하도록 조건을 설정합니다.
- 복구 목표: 적합한 key1 값을 찾고, 이를 이용해 p를 정확히 계산하는 것이 목적입니다.
결과
이 코드의 출력은 조건을 만족하는 p(원래 값)입니다.
예를 들어:
- 특정 key1 값에 대해 분모가 정확히 나눠떨어지면 p는 정수로 계산됩니다.
- 그 정수가 원래 복구해야 하는 값이 됩니다.
이 코드는 암호화/복호화 문제를 해결하는 간단한 예제로, 브루트포스 탐색을 통해 정확한 값을 복구하려는 시도를 보여줍니다.
'Dreamhack > Dreamhack Wargame (Challenge)' 카테고리의 다른 글
| [123] IT 비전공자 [dreamhack]chinese what?문제 풀기 (0) | 2025.01.11 |
|---|---|
| [122] IT 비전공자 [dreamhack]Stop before stops!문제 풀기 (0) | 2025.01.10 |
| [120] IT 비전공자 [dreamhack]Just read flag문제 풀기 (0) | 2025.01.08 |
| [119] IT 비전공자 [dreamhack][CodeEngn] Malware L08문제 풀기 (0) | 2025.01.07 |
| [118] IT 비전공자 [dreamhack]Batch Checker문제 풀기 (0) | 2025.01.06 |